Adding Rational Numbers How can a number be a rational one?! Any number could be a rational if it represents a ratio between two integers A and B where B is the denominator which doesn't equal zero. like for example, 3 over 4, 17 over 45 and 101 over 585 .. This term was first to be released by the Italian Mathematician: Giuseppe Peano. Case 1: If we are adding 2 and 3, the result is concretely 5 but, if I won't to maximize this 5 to make it equal to 5 over 7, you would try to multiply (2+3) by 1 over 7. We can distribute this as 2 over 7 plus 3 over 7 which equals 5 over 7 surely. The note here is that: in case of having a same denominator, we fix this denominator and add the numerators easily. Case 2: If we have two different denominators like 12 and 18, we look for their H.C.F which is 6 as 12= 6*2 and 18= 6*3, so we discard this 6.. so we are left with 2 and 3 where 2 is odd for 18, and 3 is odd for 12. We multiply 1/18 with 2/2 which actually equals 1 abd it doesn't change its quantity. and 1/12 with 3/3.. we get 2/36 + 3/36 = 5/36. Case 3: If we have denominators that are not equal or share a common factor, we try the general and most popular case. in the example 2/5 + 3/7, denominators 5 and 7 are odd to each other so, we try saying that: 2/5 * 7/7 and 3/7 * 5/5 equals 14/35 + 15/35 which equals 29/35 and here it is. Exercises: I) 6/7 + 5/9 II) 1/2 + 1/4 III) 5 + 3/5 IV) 1/10 + 1/5 V) 60/61 + 60/62 Answers: I) 89/63 II) 3/4 III) 28/5 IV) 3/10 V) 7380/3782 or 3690/1891 (The Hardest)
:ملخص للدرس من اعداد محمد البرديسى




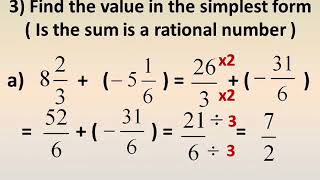

























التعليقات